题目内容
9. 如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
分析 根据平行四边形的性质得到AD∥BC,得出∠ADF=∠CFH,∠EAG=∠FCH,证出四边形BFDE是平行四边形,得出BE∥DF,证出∠AEG=∠CFH,由ASA证明△AEG≌△CFH,得出对应边相等即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CFH,∠EAG=∠FCH,
∵E、F分别为AD、BC边的中点,
∴AE=DE=$\frac{1}{2}$AD,CF=BF=$\frac{1}{2}$BC,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∴∠AEG=∠ADF,
∴∠AEG=∠CFH,
在△AEG和△CFH中,$\left\{\begin{array}{l}{∠EAG=∠FCH}&{\;}\\{AE=CF}&{\;}\\{∠AEG=∠CFH}&{\;}\end{array}\right.$,
∴△AEG≌△CFH(ASA),
∴AG=CH.
点评 本题考查了平行四边形的性质和判定,全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | (-ab3)2=a2b3 | B. | (x+3)2=x2+9 | C. | (-4)0=1 | D. | (-1)-3=1 |
20.某校校园足球训练队队员的年龄有13、14、15、16四种年龄,统计结果如表:
根据表中信息可以判断该足球训练队队员年龄的众数为( )
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数(个) | 14 | 15 | 16 | 17 |
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
17. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 垂线段最短 | B. | 经过一点有无数条直线 | ||
| C. | 经过两点,有且仅有一条直线 | D. | 两点之间,线段最短 |
4.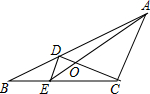 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)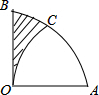 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.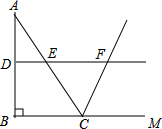 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )