题目内容
9．计算：$\sqrt{8}$-|-3$\sqrt{2}$|-（$\frac{1}{2}$）-1+2cos45°．分析 直接利用算术平方根的定义以及结合特殊角的三角函数值、绝对值的性质、负整数指数幂的性质分别化简求出答案．
解答 解：原式=2$\sqrt{2}$-3$\sqrt{2}$-2+2×$\frac{\sqrt{2}}{2}$
=-$\sqrt{2}$-2+$\sqrt{2}$
=-2．
点评 此题主要考查了算术平方根的定义以及特殊角的三角函数值、绝对值的性质、负整数指数幂的性质等知识，正确化简各数是解题关键．
练习册系列答案
相关题目
19．下列说法中正确的是（ ）
| A． | 含有一个未知数的等式是一元一次方程 | |
| B． | 未知数的次数都是1次的方程是一元一次方程 | |
| C． | 含有一个未知数，并且未知数的次数都是一次的方程是一元一次方程 | |
| D． | 2t-7=1是一元一次方程 |
20．将二次函数y=2x2-4x-1的图象向右平移3个单位，则平移后的二次函数的顶点是（ ）
| A． | （-2，-3） | B． | （4，3） | C． | （4，-3） | D． | （1，0） |
4．整数m满足$\left\{\begin{array}{l}{2m-1＞0}\\{4-2m＞-1}\end{array}\right.$，则关于x的方程m2x2-4x-2=（m+2）x2+3x+4的解为（ ）
| A． | x1=-2，x2=-$\frac{3}{2}$ | B． | x1=2，x2=$\frac{3}{2}$ | ||
| C． | x1=-$\frac{6}{7}$ | D． | x1=-2，x2=-$\frac{3}{2}$，x3=-$\frac{6}{7}$ |
18．小红制作了十张卡片，上面分别标有0～9这十个数字．从这十张卡片中随机抽取一张恰好能被3整除的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{2}{5}$ |
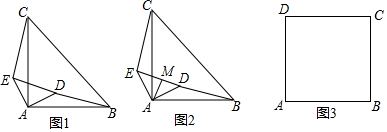
如图，在矩形ABCD中，点O在对角线AB上，以OA的长为半径的圆O与AD交于点E，且∠ACB=∠DCE，求证：CE是⊙O的切线．