题目内容
3.【问题情境】(1)如图1,△ABC、△ADE都是等腰直角三角形,连接CE、BE,F为CE的中点,连接DF,试探究DF和BE的数量关系;【猜想证明】(2)如图2,某数学兴趣小组在探究DF和BE的数量关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:当点D在AC边上时,DF=$\frac{1}{2}$BE,当点D在AB边上时,结论DF=$\frac{1}{2}$BE还成立吗?请给出证明;
【拓展延伸】(3)试验发现:不论点D在什么位置,总有DF=$\frac{1}{2}$BE,试在一般情况下(如图3)证明这个结论.
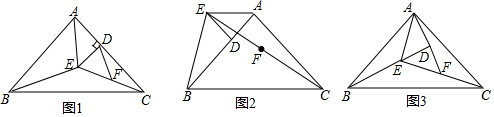
分析 【猜想证明】如图2,延长ED,交BC于N,连接AN,CN,再根据SAS判定△ABE≌△ACN,进而得出BE=CN,最后根据根据三角形的中位线,得到DF=$\frac{1}{2}$CN,等量代换即可得到结论;
【拓展延伸】如图3,与上面类似,先延长ED,交BC于N,连接AN,CN,再根据SAS判定△ABE≌△ACN,进而得出BE=CN,最后根据根据三角形的中位线,得到DF=$\frac{1}{2}$CN,等量代换即可得到结论.
解答  解:【猜想证明】(2)如图2,延长ED到N,使DN=DE,连接AN,CN,
解:【猜想证明】(2)如图2,延长ED到N,使DN=DE,连接AN,CN,
∵AD⊥EN,D是EN的中点,即AD垂直平分EN,
∴AE=AN,
又∵等腰直角三角形ADE中,∠AED=45°,
∴∠AND=45°,
∴∠EAN=90°,
又∵∠BAC=90°,
∴∠BAE=∠CAN,
∵△ABC是等腰直角三角形,
∴AB=AC,
在△ABE和△ACN中,
$\left\{\begin{array}{l}{AE=AN}\\{∠BAE=∠CAN}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACN(SAS),
∴BE=CN,
∵F是CE的中点,D是EN的中点,
∴DF是△ECN的中位线,
∴DF=$\frac{1}{2}$CN=$\frac{1}{2}$BE;
【拓展延伸】(3)证明:延长ED到N,使DN=DE,连接AN,CN,
∵AD⊥EN,D是EN的中点,即AD垂直平分EN,
∴AE=AN,
又∵等腰直角三角形ADE中,∠AED=45°,
∴∠AND=45°,
∴∠EAN=90°,
又∵∠BAC=90°,
∴∠BAE=∠CAN,
∵△ABC是等腰直角三角形,
∴AB=AC,
在△ABE和△ACN中,
$\left\{\begin{array}{l}{AE=AN}\\{∠BAE=∠CAN}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACN(SAS),
∴BE=CN,
∵F是CE的中点,D是EN的中点,
∴DF是△ECN的中位线,
∴DF=$\frac{1}{2}$CN=$\frac{1}{2}$BE.
点评 本题属于三角形综合题,主要考查了等腰直角三角形的性质,三角形中位线定理,以及全等三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造等腰直角三角形以及全等三角形,依据等腰直角三角形的性质以及全等三角形的对应边相等得出结论.解题时注意:三角形的中位线平行于第三边,并且等于第三边的一半.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{5}$ |
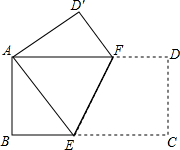 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,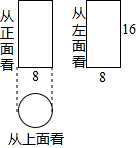 如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π)
如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π) 如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E
如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E