题目内容
1．
（1）解不等式：4x+7＜5x-2．（2）关于x的不等式x-a≥-3的解集如图所示，求a的值．
分析 （1）先移项，再合并同类项，把x的系数化为1即可；
（2）先用a表示出不等式的解集，再根据数轴上不等式的解集求出a的值即可，
解答 解：（1）移项得，4x-5x＜-2-7，
合并同类项得，-x＜-9，
把x的系数化为1得，x＞9；
（2）解不等式x-a≥-3得，x≥-3+a．
由数轴上不等式的解集可知，x≥-1，
故-3+a=-1，解得a=2．
点评 本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
11．下列说法正确的是（ ）
| A． | 2π是偶数 | B． | $\frac{31}{13}$是无理数 | ||
| C． | $\frac{\sqrt{3}}{2}$是分数 | D． | $\root{3}{25}$是无限不循环小数 |
9．下列方程中，没有实数根的方程是（ ）
| A． | x2+2x-1=0 | B． | x2+2x+1=0 | C． | x2-x+2=0 | D． | x2-x-2=0 |
16．已知△ABC的三边长分别为a，b，c，且满足（a-5）2+|b-12|+$\sqrt{c-13}$=0，则△ABC（ ）
| A． | 不是直角三角形 | B． | 是以a为斜边的直角三角形 | ||
| C． | 是以b为斜边的直角三角形 | D． | 是以c为斜边的直角三角形 |
6．
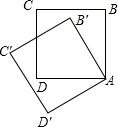如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（ ）
如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
如图，将两根钢条AB、CD的中点O连在一起，使AB、CD可以绕点O自由转动，就做成一个测量工件，则AC的长等于内槽宽BD，则判定△OBD≌△OAC的理由是（ ）