题目内容
13.(1)如图1,已知△ABC中,AB=AC,过点A作射线AM,使AM⊥BC交BC于点D.(要求:尺规作图,不写作法但保留作图痕迹)(2)如图2,已知△ABC中,点D是BC的中点,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.求证:△ABC是等腰三角形.

分析 (1)过点A作AD⊥BC于点D,如图1;
(2)如图2,先利用角平分线的性质得到DE=DF,则根据“HL”可证明Rt△BDE≌Rt△CDF,所以∠B=∠C,然后根据等腰三角形的判定定理可判定△ABC是等腰三角形.
解答 解:(1)如图1,AD为所作;
(2)如图2,∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,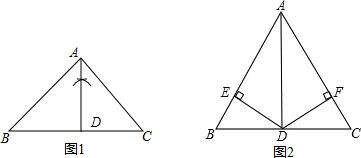
∴DE=DF,
∵D为BC的中点,
∴BD=CD,
在Rt△BDE和Rt△CDF中
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴△ABC是等腰三角形.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.也考查了等腰三角形的判定.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
8. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )| A. | AB=CD | B. | BO=OD | C. | ∠BAD=∠BCD | D. | AB⊥AC |
18.下列选项是无理数的为( )
| A. | -$\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1415926 | D. | -π |
5.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 打开电视机,正在播放动画片 | |
| C. | 两边及其夹角对应相等的两个三角形全等 | |
| D. | 三根长度为2cm、2cm、4cm的木棒能摆成三角形 |
 小明骑自行车从家里出发到野外郊游,从家出发1小时后到植物园,游玩一段时间后按原速前往动物园.小明离家1小时50分钟后,爸爸驾车沿相同路线前往动物园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.
小明骑自行车从家里出发到野外郊游,从家出发1小时后到植物园,游玩一段时间后按原速前往动物园.小明离家1小时50分钟后,爸爸驾车沿相同路线前往动物园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.

 (1)解不等式:4x+7<5x-2.
(1)解不等式:4x+7<5x-2. (1)先化简再求值:(2x-1)2+(x+2)(x-2)-4x(x-1),其中x=2.
(1)先化简再求值:(2x-1)2+(x+2)(x-2)-4x(x-1),其中x=2.