题目内容
6.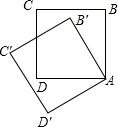 如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 设B′C′与CD相交于点E,然后利用“HL”证明Rt△ADE和Rt△AB′E全等,根据全等三角形对应角相等可得∠EAB′=∠EAD,再根据旋转角求出∠BAB′=30°,再解直角三角形求出ED的长,然后利用三角形的面积公式列式进行计算即可得解.
解答 解:如图,设B′C′与CD相交于点E,
在Rt△ADE和Rt△AB′E,
$\left\{\begin{array}{l}{AE=AE}\\{AD=AB′}\end{array}\right.$,
∴Rt△ADE≌Rt△AB′E(HL),
∴∠EAB′=∠EAD,
∵旋转角为30°,
∴∠BAB′=30°,
∴∠EAD=$\frac{1}{2}$(90°-30°)=30°,
在Rt△ADE中,ED=ADtan30°=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,
∴这个风筝的面积=2×S△ADE=2×$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$;
故选:B.
点评 本题考查了旋转的性质,主要利用了全等三角形的判定与性质,等腰直角三角形的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16. 如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )
如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )
 如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )
如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )| A. | 中位数是55 | B. | 众数是60 | C. | 方差是29 | D. | 平均数是54 |
17.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
11.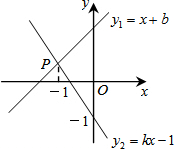 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
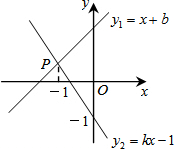 如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )
如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )| A. | x≥-1 | B. | x>-1 | C. | x≤-1 | D. | x<-1 |
18.下列选项是无理数的为( )
| A. | -$\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1415926 | D. | -π |
15.已知∠1=20°,则∠1的余角度数是( )
| A. | 70° | B. | 80° | C. | 150° | D. | 160° |
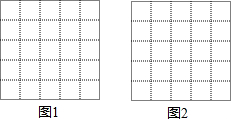 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. (1)解不等式:4x+7<5x-2.
(1)解不等式:4x+7<5x-2.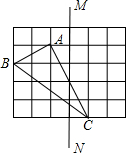 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题.