题目内容
9.下列方程中,没有实数根的方程是( )| A. | x2+2x-1=0 | B. | x2+2x+1=0 | C. | x2-x+2=0 | D. | x2-x-2=0 |
分析 分别求出每一个方程中判别式△的值,如果△<0,那么一元二次方程没有实数根.
解答 解:A、∵△=4+4=8>0,∴方程有两个不相等的两个实数根;
B、∵△=4-4=0,∴方程有两个相等的两个实数根;
C、∵△=1-8=-7<0,∴方程没有实数根;
D、∵△=1+8=9>0,∴方程有两个不相等的两个实数根;
故选C.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.下列方程后所列出的解不正确的是( )
| A. | $\frac{x}{2}$-1=x,x=-2 | B. | 2-x=$\frac{1}{2}$+x,x=$\frac{3}{4}$ | C. | -$\frac{2}{3}$x=$\frac{3}{2}$,x=-$\frac{3}{4}$ | D. | -$\frac{x}{2}$+$\frac{2}{3}$=1,x=-$\frac{2}{3}$ |
20.-a6÷(-a)2的值是( )
| A. | -a4 | B. | a4 | C. | -a3 | D. | a3 |
17.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
18.下列选项是无理数的为( )
| A. | -$\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1415926 | D. | -π |
19.点A(-4,0)与点B(4,0)是( )
| A. | 关于y轴对称 | B. | 关于x轴对称 | ||
| C. | 关于坐标轴都对称 | D. | 以上答案都错 |


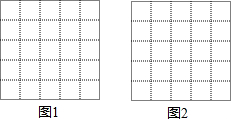 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. (1)解不等式:4x+7<5x-2.
(1)解不等式:4x+7<5x-2.