题目内容
6.若(a+1)2+|b-2012|=0,则b-a2=2011.分析 首先根据任何数的平方、绝对值都是非负数,几个非负数的和是0,则每个数等于0即可列方程求得a和b的值,进而求得代数式的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{a+1=0}\\{b-2012=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2012}\end{array}\right.$,
则原式=2012-(-1)2=2011.
故答案是:2011.
点评 本题考查了非负数的性质,几个非负数的和是0,则每个数等于0,初中范围内的非负数有:数的平方、绝对值和算术平方根.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
1.函数y=kx+b图象经过一、三、四象限,则函数y=bx-k图象经过( )
| A. | 一、二、四象限 | B. | 一、二、三象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
15.已知实数a、b、c满足a+b+c=0,a>b>c,若直线y1=ax+b+c经过抛物线y2=ax2+bx+c的顶点,则下列结论错误的是( )
| A. | 直线y1经过一、三、四象限 | |
| B. | 抛物线y2必经过点(1,0) | |
| C. | 当x>1或x<0时,y2>y1 | |
| D. | 当x>-1时,y1、y2均随x的增大而增大 |
16. 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )| A. | (2$\sqrt{3}$,30°) | B. | (60°,2$\sqrt{3}$) | C. | (30°,4) | D. | (30°,2$\sqrt{3}$) |
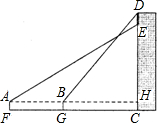 如图所示,为了知道楼房CD外墙上一电子屏的高度DE是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作;在A处测得点E的仰角为31°,在B出测得点D的仰角为50°,A、B、H共线,且AH⊥CD于点H,AB为20米,测角仪的高度(AF、BG)为1.6米.已知楼房CD高为34.6米,根据测量数据,请求出DE的高度.(参考数据:tan31°≈0.6,tan50°≈1.2)
如图所示,为了知道楼房CD外墙上一电子屏的高度DE是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作;在A处测得点E的仰角为31°,在B出测得点D的仰角为50°,A、B、H共线,且AH⊥CD于点H,AB为20米,测角仪的高度(AF、BG)为1.6米.已知楼房CD高为34.6米,根据测量数据,请求出DE的高度.(参考数据:tan31°≈0.6,tan50°≈1.2)