题目内容
16. 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )| A. | (2$\sqrt{3}$,30°) | B. | (60°,2$\sqrt{3}$) | C. | (30°,4) | D. | (30°,2$\sqrt{3}$) |
分析 过B作BC⊥x轴于C,根据正六边形的性质,得到△ACB与△BCO都是含30°的直角三角形,根据含30°的直角三角形的性质先得到BC的长度,再得到OB的长度,然后根据“极坐标”的定义写出即可.
解答  解:如图,过B作BC⊥x轴于C,
解:如图,过B作BC⊥x轴于C,
∵六边形是正六边形,
∴∠BAC=60°,AO=AB,
∴∠ABC=30°,∠AOB=∠ABO=30°,
∴在Rt△ACB中,BC=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$,
在Rt△BCO中,BO=2BC=2$\sqrt{3}$.
∴正六边形的顶点B的极坐标应记为(30°,2$\sqrt{3}$).
故选:D.
点评 本题考查了正多边形,坐标确定位置,主要利用了正六边形的性质,读懂题目信息,理解“极坐标”的定义是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
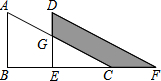 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$. 已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h).
已知A,B两地相距30km,甲骑自行车以15km/h的速度从A地到B地,同时,乙骑摩托车以30km/h的速度从B地到A地,到达A地后立即按原路原速返回,设甲、乙两人离B地的距离分别为y甲(km),y乙(km),行驶时间为t(h). 如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.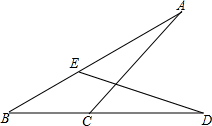 如图,已知AC=DE,AB=BD,求证:BC=BE.
如图,已知AC=DE,AB=BD,求证:BC=BE.