题目内容
15.已知实数a、b、c满足a+b+c=0,a>b>c,若直线y1=ax+b+c经过抛物线y2=ax2+bx+c的顶点,则下列结论错误的是( )| A. | 直线y1经过一、三、四象限 | |
| B. | 抛物线y2必经过点(1,0) | |
| C. | 当x>1或x<0时,y2>y1 | |
| D. | 当x>-1时,y1、y2均随x的增大而增大 |
分析 根据a+b+c=0,得出抛物线过点(1,0),再根据a>b>c,得出a>0,b>0,c<0,再进行判断即可.
解答 解:∵a+b+c=0,a>b>c,
∴直线y1=ax+b+c和抛物线y2=ax2+bx+c必经过点(1,0),
∵a>b>c,
∴a>0,b>0,c<0,
∴直线y1经过一、三、四象限,
∴当x>1或x<0时,y2>y1,
故选D.
点评 本题考查了一次函数的性质,二次函数的性质,掌握二次函数y=ax2+bx+c系数符号的确定以及抛物线开口方向、对称轴、与y轴的交点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
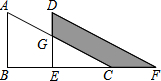 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.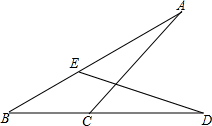 如图,已知AC=DE,AB=BD,求证:BC=BE.
如图,已知AC=DE,AB=BD,求证:BC=BE.