题目内容
19.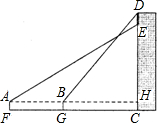 如图所示,为了知道楼房CD外墙上一电子屏的高度DE是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作;在A处测得点E的仰角为31°,在B出测得点D的仰角为50°,A、B、H共线,且AH⊥CD于点H,AB为20米,测角仪的高度(AF、BG)为1.6米.已知楼房CD高为34.6米,根据测量数据,请求出DE的高度.(参考数据:tan31°≈0.6,tan50°≈1.2)
如图所示,为了知道楼房CD外墙上一电子屏的高度DE是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作;在A处测得点E的仰角为31°,在B出测得点D的仰角为50°,A、B、H共线,且AH⊥CD于点H,AB为20米,测角仪的高度(AF、BG)为1.6米.已知楼房CD高为34.6米,根据测量数据,请求出DE的高度.(参考数据:tan31°≈0.6,tan50°≈1.2)
分析 首先由题意知∠EAH=31°,∠DBH=50°,CH=AF=1.6,则可求得DH的长,然后由在Rt△DBH中,tan50°=$\frac{DH}{BH}$,求得BH的长,继而求得AH的长,然后在Rt△EAH中,求得EH的长,则可求得答案.
解答  解:由题意知∠EAH=31°,∠DBH=50°,CH=AF=1.6,
解:由题意知∠EAH=31°,∠DBH=50°,CH=AF=1.6,
∴DH=DC-CH=34.6-1.6=33,
在Rt△DBH中,
∵tan50°=$\frac{DH}{BH}$=$\frac{33}{BH}$,
∴BH=$\frac{33}{tan50°}$≈$\frac{33}{1.2}$=27.5,
∴AH=27.5+20=47.5.
在Rt△EAH中,
∵tan31°$\frac{EH}{AH}$=$\frac{EH}{47.5}$,
∴EH=47.5×tan31°≈28.5,
∴DE=DH-EH≈33-28.5=4.5(米).
答:DE的高度约为4.5米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
7.某玩具店试销售一种进价为20元的新型玩具,根据物价部门规定:该玩具售价不得超过90元.在连续七天的试销售过程中,玩具店就销售量y(个)与售价x(元)之间的变化关系做了如表记录.
(1)运用所学过的函数知识,试判断y与x之间的函数关系,并求y与x的函数关系式;
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 售价x | 30 | 30 | 35 | 40 | 40 | 40 | 45 |
| 销售量y | 100 | 100 | 95 | 90 | 90 | 90 | 85 |
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
14.如图所示的几何体的左视图是( )


| A. |  | B. |  | C. |  | D. |  |
11.下列各数中,最小的数是( )
| A. | -3 | B. | 1 | C. | 0 | D. | 2 |
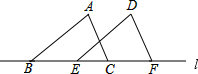 已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( )
已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( )