题目内容
14.已知四边形ABCD对角线相交于点O,若在线段BD上任意取一点(不与点B,O,D重合),并与A、C连接,如图1,则三角形个数为15个;若在线段BD上任意取两点(不与点B、O、D重合)如图2,则三角形个数为24个;若在线段BD上任意取三点(不与点B、O、D重合)如图3,则三角形个数为35个…以此规律,则图5中三角形的个数为( )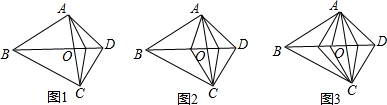
| A. | 48 | B. | 56 | C. | 61 | D. | 63 |
分析 根据第一个图形的个数,第二个图形的个数,第三个图形的个数,得到第n个图形的个数=(3+n)2-1,于是得到结论.
解答 解:第一个图形的个数=15=(3+1)2-1,
第二个图形的个数=24=(3+2)2-1,
第三个图形的个数=36=(3+3)2-1,
…
∴第n个图形的个数=(3+n)2-1,
∴第五个图形的个数=(3+5)2-1=63,
故选D.
点评 本题考查了规律型:图形的变化类,找出规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某玩具店试销售一种进价为20元的新型玩具,根据物价部门规定:该玩具售价不得超过90元.在连续七天的试销售过程中,玩具店就销售量y(个)与售价x(元)之间的变化关系做了如表记录.
(1)运用所学过的函数知识,试判断y与x之间的函数关系,并求y与x的函数关系式;
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 售价x | 30 | 30 | 35 | 40 | 40 | 40 | 45 |
| 销售量y | 100 | 100 | 95 | 90 | 90 | 90 | 85 |
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
19.计算(x+3)•(x-3)正确的是( )
| A. | x2+9 | B. | 2x | C. | x2-9 | D. | x2-6 |
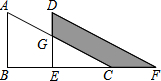 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.