题目内容
阅读理解:
对于任意正整数a,b,∵(
-
)2≥0,∴a-2
+b≥0,∴a+b≥2
,只有当a=b时,等号成立;结论:在a+b≥2
(a、b均为正实数)中,只有当a=b时,a+b有最小值2
.
根据上述内容,回答下列问题:
(1)若a+b=9,
≤ ;
(2)若m>0,当m为何值时,m+
有最小值,最小值是多少?
对于任意正整数a,b,∵(
| a |
| b |
| ab |
| ab |
| ab |
| ab |
根据上述内容,回答下列问题:
(1)若a+b=9,
| ab |
(2)若m>0,当m为何值时,m+
| 1 |
| m |
考点:二次根式的应用
专题:阅读型
分析:(1)根据a+b≥2
(a、b均为正实数),进而得出即可;
(2)根据a+b≥2
(a、b均为正实数),进而得出即可.
| ab |
(2)根据a+b≥2
| ab |
解答:解:(1)∵a+b≥2
(a、b均为正实数),
∴a+b=9,则a+b≥2
,即
≤
;
故答案为:
;
(2)由(1)得:m+
≥2
,
即m+
≥2,当m=
时,m=1(负数舍去),
故m+
有最小值,最小值是2.
| ab |
∴a+b=9,则a+b≥2
| ab |
| ab |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
(2)由(1)得:m+
| 1 |
| m |
m×
|
即m+
| 1 |
| m |
| 1 |
| m |
故m+
| 1 |
| m |
点评:此题主要考查了二次根式的应用,根据题意结合a+b≥2
(a、b均为正实数)求出是解题关键.
| ab |

练习册系列答案
相关题目
若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
| A、1个或2个或3个 |
| B、0个或1个或2个或3个 |
| C、1个或2个 |
| D、以上都不对 |
 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长. 如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=
如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=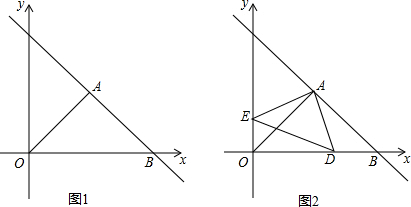
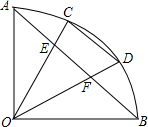 如图,∠AOB=90°,CD是
如图,∠AOB=90°,CD是
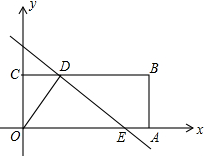 如图,四边形OABC是矩形,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
如图,四边形OABC是矩形,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-