题目内容
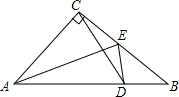 如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:(1)AE垂直平分CD;
(2)AB=AC+CE.
考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:(1)求出∠CAE=∠DAE,∠ACE=∠ADE=90°,根据AAS推出△ACE≌△ADE,根据全等得出AC=AD,DE=EC,根据等腰三角形的性质得出即可.
(2)求出BD=DE,由(1)得出AC=AD,CE=DE=BD,即可得出答案.
(2)求出BD=DE,由(1)得出AC=AD,CE=DE=BD,即可得出答案.
解答:证明:(1)∵AE是角平分线,
∴∠CAE=∠DAE,
∵ED⊥AB,
∴∠ACE=∠ADE=90°,
在△ACE和△ADE中,
,
∴△ACE≌△ADE(AAS),
∴AC=AD,DE=EC,
∵∠CAE=∠DAE,
∴AE垂直平分CD;
(2)∵在△ABC中,∠ACB=90°,AC=BC,
∴∠B=45°,
∵ED⊥AB,
∴∠EDB=90°,
∴∠DEB=∠B=45°,
∴BD=DE,
∵AC=AD,CE=DE=BD,
∴AB=AD+BD=AC+CE.
∴∠CAE=∠DAE,
∵ED⊥AB,
∴∠ACE=∠ADE=90°,
在△ACE和△ADE中,
|
∴△ACE≌△ADE(AAS),
∴AC=AD,DE=EC,
∵∠CAE=∠DAE,
∴AE垂直平分CD;
(2)∵在△ABC中,∠ACB=90°,AC=BC,
∴∠B=45°,
∵ED⊥AB,
∴∠EDB=90°,
∴∠DEB=∠B=45°,
∴BD=DE,
∵AC=AD,CE=DE=BD,
∴AB=AD+BD=AC+CE.
点评:本题考查了全等三角形的性质和判定,等腰直角三角形的性质的应用,能推出△ACE≌△ADE是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,PA、PB、CD分别与⊙O相切于A、B、E,若∠COD=50°,则∠P=( )
如图,PA、PB、CD分别与⊙O相切于A、B、E,若∠COD=50°,则∠P=( )| A、80° | B、55° |
| C、130° | D、65° |
将下面的抛物线向上平移3个单位,再向左平移2个单位后能得到抛物线y=3x2的是( )
| A、y=3(x+2)2+3 |
| B、y=3(x-2)2+3 |
| C、y=3(x+2)2-3 |
| D、y=3(x-2)2-3 |
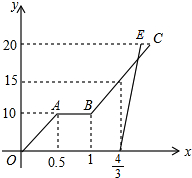 小张骑自行车,小李骑摩托车沿相同路线由甲地到乙地,小张先出发,骑行一段时间后因自行车出现故障进行维修,修好后按原来的速度继续骑行,小张离开甲地1小时20分后,小李开始骑行,如图是他们两人离开甲地的距离(千米)与(小时)之间的函数关系图象,已知小李的骑行速度是小张的3倍.
小张骑自行车,小李骑摩托车沿相同路线由甲地到乙地,小张先出发,骑行一段时间后因自行车出现故障进行维修,修好后按原来的速度继续骑行,小张离开甲地1小时20分后,小李开始骑行,如图是他们两人离开甲地的距离(千米)与(小时)之间的函数关系图象,已知小李的骑行速度是小张的3倍.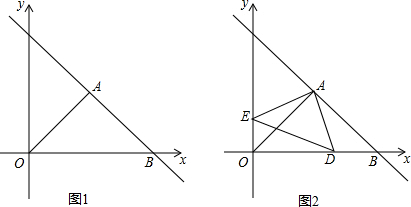
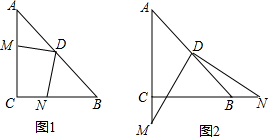 如图1,在△ABC中,CA=CB,∠ACB=90°,D为AB的中点,M,N分别为AC,BC上的点,且DM⊥DN.
如图1,在△ABC中,CA=CB,∠ACB=90°,D为AB的中点,M,N分别为AC,BC上的点,且DM⊥DN.