题目内容
12．如图，①中线段的条数为10条；在①中加一条横截线得到图②，图②中线段的条数为24；在①中加两条横截线得到图③，图③中线段的条数为42条；在①中加七条横截线得到图⑧，则图⑧中线段条数为（ ）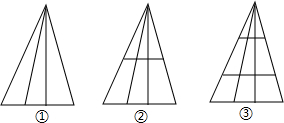
| A． | 154 | B． | 192 | C． | 234 | D． | 252 |
分析 由图可知：图①中线段的条数为4+（3+2+1）=10条；图②中线段的条数为4×（1+2）+2×（3+2+1）=24；图③中线段的条数为4×（1+2+3）+3×（3+2+1）=42条；…由此得出图n中线段的条数为4×（1+2+3+…+n）+n×（3+2+1）=2n2+8n条；进一步代入求得答案即可．
解答 解：∵图①中线段的条数为4+（3+2+1）=10条；
图②中线段的条数为4×（1+2）+2×（3+2+1）=24；
图③中线段的条数为4×（1+2+3）+3×（3+2+1）=42条；
∴图n中线段的条数为4×（1+2+3+…+n）+n×（3+2+1）=2n2+8n条；
∴图⑧中线段的条数为128+64=192条．
故选：B．
点评 此题考查图形的变化规律，找出图形之间的联系，得出数字的运算规律，利用规律解决问题．
练习册系列答案
相关题目
2．
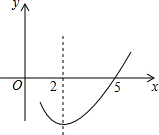二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（5，0），对称轴为直线x=2，则下列结论中正确的是（ ）
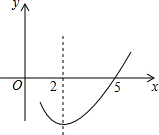二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（5，0），对称轴为直线x=2，则下列结论中正确的是（ ）| A． | 当x＞2时，y随x增大而减小 | B． | 4a=b | ||
| C． | 图象过点（-1，0） | D． | 9a+3b+c＞0 |
如图，⊙O中弦AB，CD相交于点P，已知AP=3，BP=2，CP=1，则DP=6．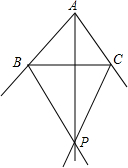
已知，如图所示，在△ABC中，PB，PC分别是△ABC的两个外角的平分线，求证：AP平分∠BAC．