题目内容
3.从-3,-2,-1,0,1,2这六个数中,任意抽取一个数,作为反比例函数y=$\frac{{m}^{2}-5}{x}$和二次函数y=(m+1)x2+mx+1中的m的值,恰好使所得的反比例函数在每个象限内,y随x的增大而增大,且二次函数的图象开口向上的概率为$\frac{1}{2}$.分析 使所得的反比例函数在每个象限内,y随x的增大而增大,且二次函数的图象开口向上的m的个数,然后利用概率公式求解即可.
解答 解:∵反比例函数y=$\frac{{m}^{2}-5}{x}$恰好使所得的反比例函数在每个象限内,y随x的增大而增大,
∴m2-5<0,
解得:-$\sqrt{5}$<m<$\sqrt{5}$,
∵二次函数y=(m+1)x2+mx+1的开口向上,
∴m+1>0,
解得:m>-1,
∴满足条件的m的值有0,1,2三个,
∴恰好使所得的反比例函数在每个象限内,y随x的增大而增大,且二次函数的图象开口向上的概率为$\frac{3}{6}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,关键是求出符合条件的数的个数.

练习册系列答案
相关题目
13.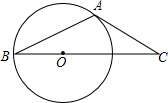 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
18.下列说法中不正确的是( )
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m+n=6 | |
| D. | 任意打开七年级下册数学教科书,正好是97页是确定事件 |
8.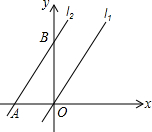 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x、y轴分别交于点A、B,且l1∥l2,OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
12.如图,①中线段的条数为10条;在①中加一条横截线得到图②,图②中线段的条数为24;在①中加两条横截线得到图③,图③中线段的条数为42条;在①中加七条横截线得到图⑧,则图⑧中线段条数为( )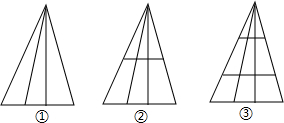

| A. | 154 | B. | 192 | C. | 234 | D. | 252 |
13.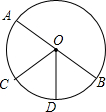 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )| A. | 30° | B. | 45° | C. | 60° | D. | 以上都不正确 |
 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(30°角所对的直角边是斜边的一半)
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(30°角所对的直角边是斜边的一半)