题目内容
2.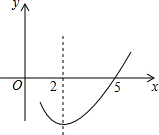 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )| A. | 当x>2时,y随x增大而减小 | B. | 4a=b | ||
| C. | 图象过点(-1,0) | D. | 9a+3b+c>0 |
分析 根据二次函数的性质对A进行判断;根据抛物线的对称轴方程可对B进行判断;根据抛物线与x轴的交点问题和抛物线的对称性可判断抛物线与x轴的另一个交点坐标为(-1,0),则可对C进行判断;利用x=3所对应的函数值为负数可对D进行判断.
解答 解:A、抛物线的对称轴为直线x=2,则x>2时,y随x增大而增大,所以A选项错误;
B、抛物线的对称轴为直线x=-$\frac{b}{2a}$=2,则b=-4a,所以B选项错误;
C、抛物线与x轴的一个交点坐标为(5,0),而对称轴为直线x=2,则抛物线与x轴的另一个交点坐标为(-1,0),所以C选项正确;
D、当x=3时,y<0,即9a+3b+c<0,所以D选项错误.
故选C.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键是运用数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.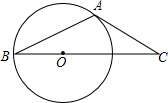 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
 如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )
如图,在⊙O中,AB是弦,若过点A的切线交BO的延长线于点C,∠C=40°,则∠BAC的大小为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
10.下列说法其中正确的有( )
(1)最小的正整数是1,最大的负整数是-1;
(2)相反数等于它本身的数只有0,倒数等于它本身的数是±1
(3)绝对值等于它本身的数是非负数,绝对值等于它的相反数的数是非正数
(4)绝对值相等的两个数一定相等,绝对值不相等的两个数一定不相等.
(1)最小的正整数是1,最大的负整数是-1;
(2)相反数等于它本身的数只有0,倒数等于它本身的数是±1
(3)绝对值等于它本身的数是非负数,绝对值等于它的相反数的数是非正数
(4)绝对值相等的两个数一定相等,绝对值不相等的两个数一定不相等.
| A. | (1),(2),(3) | B. | (2),(3),(4) | C. | (1),(3),(4) | D. | (1),(2),(3),(4) |
 如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.
如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.