题目内容
1.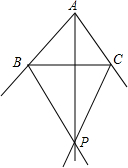 已知,如图所示,在△ABC中,PB,PC分别是△ABC的两个外角的平分线,求证:AP平分∠BAC.
已知,如图所示,在△ABC中,PB,PC分别是△ABC的两个外角的平分线,求证:AP平分∠BAC.
分析 作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,根据角平分线性质得出PM=PN,PN=PE,推出PM=PE,根据角平分线性质推出即可.
解答  证明:作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,
证明:作PM⊥AC于M,PN⊥BC于N,PE⊥AB于E,
∵PB、PC分别是△ABC的外角平分线,
∴PM=PN,PN=PE,
∴PM=PE,
∵PM⊥AC,PE⊥AB,
∴点P在∠A的平分线上,
∴AP平分∠BAC.
点评 本题考查了角平分线性质的应用,熟知角平分线上的点到角两边的距离相等是解题的关键.

练习册系列答案
相关题目
12.如图,①中线段的条数为10条;在①中加一条横截线得到图②,图②中线段的条数为24;在①中加两条横截线得到图③,图③中线段的条数为42条;在①中加七条横截线得到图⑧,则图⑧中线段条数为( )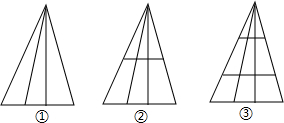

| A. | 154 | B. | 192 | C. | 234 | D. | 252 |
9.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数(单位:公里)如下:
如果设小明9:00时看到的两位数的十位数字为x,个位数字为y.那么:
(1)小明9:00时看到的两位数为10x+y;
(2)小明9:48时看到的两位数为10y+x;11:00时看到的两位数为100x+y;
(3)请你列二元一次方程求小明在9:00时看到里程碑上的两位数.
| 时刻 | 9:00 | 9:48 | 11:00 |
| 里程碑上的数 | 是一个两位数,它的两个数字之和为6 | 也是一个两位数,十位与个位数字与9:00时所看到的正好互换了 | 是一个三位数,比9:00时看到的两位数的数字中间多了个0 |
(1)小明9:00时看到的两位数为10x+y;
(2)小明9:48时看到的两位数为10y+x;11:00时看到的两位数为100x+y;
(3)请你列二元一次方程求小明在9:00时看到里程碑上的两位数.
13.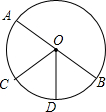 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )| A. | 30° | B. | 45° | C. | 60° | D. | 以上都不正确 |
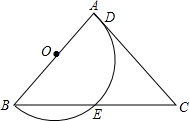 如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.
如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.