题目内容
7.已知△ABC,AD为角平分线,∠BAC=60°,将△ADC沿直线AD翻折,点C′与C相对应.若AC=4,BC′=2,求△ABC的面积.分析 如图所示:过点B作BE⊥AC,垂足为E.由翻折的性质和角平分线的定义可知∠C′AD=∠BAD,点C′、B、A在一条直线上,从而可求得AB=2,然后求得BE=$\sqrt{3}$,最后依据三角形的面积公式求解即可.
解答 解:如图所示:过点B作BE⊥AC,垂足为E.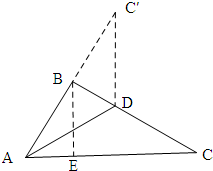
由翻折的性质可知:∠C′AD=∠CAD,AC′=AC=4.
∵AD是∠BAC的角平分线,
∴∠BAD=DAC.
∴∠C′AD=∠BAD.
∴点C′、B、A在一条直线上.
∵AC′=AC=4,BC′=2,
∴AB=2.
∵BE⊥AC,∠BAC=60°,
∴BE=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}×2$=$\sqrt{3}$.
∴${S}_{△ABC}=\frac{1}{2}•AC•BE$=$\frac{1}{2}×4×\sqrt{3}$=2$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数,证得点C′、B、A在一条直线上是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法中不正确的是( )
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m+n=6 | |
| D. | 任意打开七年级下册数学教科书,正好是97页是确定事件 |
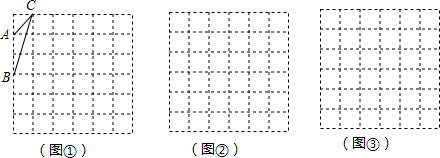
 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(30°角所对的直角边是斜边的一半)
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(30°角所对的直角边是斜边的一半)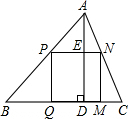 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.