题目内容
7.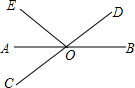 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=72°,求∠BOD的度数;
(2)若∠DOE=2∠AOC,判断射线OE,OD的位置关系并说明理由.
分析 (1)根据角平分线的性质可得∠AOC=$\frac{1}{2}$∠EOC=36°,再根据对顶角相等可得∠BOD的度数;
(2)根据题意可得∠DOE=∠EOC,再根据∠DOE+∠EOC=180°可得∠DOE的度数,进而可得OE⊥OD.
解答 (1)∵OA平分∠EOC,∠EOC=72°,
∴∠AOC=$\frac{1}{2}$∠EOC=36°(角平分线的定义),
∴∠BOD=∠AOC=36°(对顶角相等);
(2)OE⊥OD.理由如下:
∵∠DOE=2∠AOC,OA平分∠EOC,
∴∠DOE=∠EOC,
又∠DOE+∠EOC=180°,
∴∠DOE=∠EOC=90°,
∴OE⊥OD(垂直的定义).
点评 此题主要考查了角平分线定义,以及对顶角和邻补角的性质,关键是掌握对顶角相等,邻补角互补.

练习册系列答案
相关题目
2.甲乙两家商场平时以同样的价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
(Ⅱ)分别就两家商场的让利方式,写出y关于x的函数解析式;
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 180 | 200 | 242 |
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
 如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.
如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.