题目内容
12.计算(1)$\frac{1}{2}$($\sqrt{2}$+$\sqrt{3}$)-$\frac{3}{4}$($\sqrt{2}$+$\sqrt{27}$)
(2)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$)
(3)在Rt△ABC中∠C=90°,c=25,b=15,求a.
分析 (1)先去括号化简二次根式,再合并同类二次根式即可.
(2)先去括号并且化简二次根式,然后合并同类二次根式即可.
(3)根据勾股定理即可计算.
解答 解:(1)原式=$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$$\sqrt{3}$-$\frac{3}{4}$$\sqrt{2}$-$\frac{9}{4}$$\sqrt{3}$
=(-$\frac{3}{4}$+$\frac{1}{2}$)$\sqrt{2}$+($\frac{1}{2}$-$\frac{9}{4}$)$\sqrt{3}$
=-$\frac{1}{4}$$\sqrt{2}$-$\frac{7}{4}$$\sqrt{3}$.
(2)原式=2$\sqrt{6}$-$\frac{1}{2}$$\sqrt{2}$-$\frac{1}{4}$$\sqrt{2}$-$\sqrt{6}$
=$\sqrt{6}$-$\frac{3}{4}$$\sqrt{2}$.
(3)在Rt△ABC中,∵∠C=90°,c=25,b=15,
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{2{5}^{2}-1{5}^{2}}$=$\sqrt{(25+15)(25-15)}$=$\sqrt{400}$=20.
点评 本题考查二次根式的化简、勾股定理等知识,解题的关键是掌握二次根式的混合运算的法则,会化简二次根式,属于中考常考题型.

练习册系列答案
相关题目
3.某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
| 售价x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
20.某公园购进一批平均高度为2m的某种树苗.为了掌握树的生长情况,树苗栽种后,园林工作者对其进行了几年的观测,并记录了每年末这种树的平均高度,如表:
(1)这种树从栽种第几年开始,生长变得缓慢?
(2)栽种后的前4年,每年生长多少米?第5年后每年生长多少米?
(3)请写出栽种后的前4年,树高h1(m)与栽种的时间t(年)之间的函数关系式;
(4)请写出栽种第5年以后,树高h2(m)与栽种后的时间t(年)之间的函数关系式;
(5)这种树按表中的生长速度,求出第11年末树高是多少米?
| 栽后时间/年 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 树高/m | 2.0 | 2.6 | 3.2 | 3.8 | 4.4 | 4.8 | 5.2 | 5.6 | 6.0 | … |
(2)栽种后的前4年,每年生长多少米?第5年后每年生长多少米?
(3)请写出栽种后的前4年,树高h1(m)与栽种的时间t(年)之间的函数关系式;
(4)请写出栽种第5年以后,树高h2(m)与栽种后的时间t(年)之间的函数关系式;
(5)这种树按表中的生长速度,求出第11年末树高是多少米?

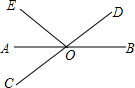 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC. 在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).
在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3). 如图,已知直线AB与CD相交于点O,OA平分∠EOC,若∠BOD=35°,求∠EOC的度数.
如图,已知直线AB与CD相交于点O,OA平分∠EOC,若∠BOD=35°,求∠EOC的度数.