题目内容
17.若二次函数y=-x2+bx+c图象的最高点是(-1,-3),则b+c的值为-6.分析 根据抛物线y=-x2+bx+c的最高点为(-1,-3)可知x=-$\frac{b}{2a}$=-1,当x=-1时,y=-3,分别求出b、c的值,进而可得出结论.
解答 解:∵抛物线y=-x2+bx+c的最高点为(-1,-3),
∴$\left\{\begin{array}{l}{-\frac{b}{-2}=-1}\\{-3=-1-b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-4}\end{array}\right.$,
∴b+c=-6.
故答案为-6.
点评 本题考查的是二次函数的最值,熟知二次函数的顶点式是解答此题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.在同一个平面内有三条直线,若有且只有两条直线平行,则它们( )
| A. | 没有交点 | B. | 只有一个交点 | C. | 有两个交点 | D. | 有三个交点 |
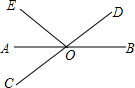 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.



 如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是35°.
如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是35°. 如图,已知直线AB与CD相交于点O,OA平分∠EOC,若∠BOD=35°,求∠EOC的度数.
如图,已知直线AB与CD相交于点O,OA平分∠EOC,若∠BOD=35°,求∠EOC的度数. 已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.
已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.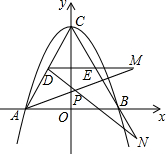 如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变. 其中正确的是( )
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,DE是正三角形ABC的中位线.动点M,N分别从D、E出发,沿着射线DE与射线EB方向移动相同的路程,连结AM,DN交于P点.则下列结论:①ac=-3;②AM=DN;③无论M,N处何位置,∠APN的大小始终不变. 其中正确的是( )