题目内容
19．已知x=$\sqrt{3}$+2，y=$\sqrt{3}$-2，求x2+2xy+y2的值．分析 先求出x+y的值，再根据完全平方公式把x2+2xy+y2变形为（x+y）2，再代值计算即可．
解答 解：∵x=$\sqrt{3}$+2，y=$\sqrt{3}$-2，
∴x+y=$\sqrt{3}$+2+$\sqrt{3}$-2=2$\sqrt{3}$，
∴x2+2xy+y2=（x+y）2=（2$\sqrt{3}$）2=12．
点评 此题考查了二次根式的化简求值，关键是根据完全平方公式把要求的式子进行变形，是一道基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
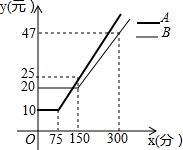某通讯公司推出A、B两种手机话费套餐，这两种套餐每月都有一定的固定费用和免费通话时间，超过免费通话时间的部分收费标准为：A套餐a元/分，B套餐b元/分，使用A、B两种套餐的通话费用y（元）与通话时间x（分）之间的函数图象如图所示．
10．
如图，平面直角坐标系中，已知点B（2，1），过点B作BA⊥x轴，垂足为A，若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点，则实数k的取值范围是（ ）
如图，平面直角坐标系中，已知点B（2，1），过点B作BA⊥x轴，垂足为A，若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点，则实数k的取值范围是（ ）| A． | -2＜k＜0 | B． | -2＜k＜$\frac{1}{8}$ | C． | -2＜k＜-1 | D． | -2＜k＜$\frac{1}{4}$ |
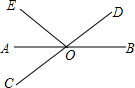如图，直线AB，CD相交于点O，OA平分∠EOC．
在一次寻宝游戏中，寻宝人找到了如图所示的两个标志，点A（2，3）、B（4，1），这两个标志点到“宝藏”点的距离都是2，则“宝藏”点的坐标是（2，1）和（4，3）．
已知：如图，在正方形ABCD中，点E、F分别在边BC和CD上，∠BAE=∠DAF．联结AC交EF于点O，延长OC至点M，联结EM、FM．