题目内容
18.正比例函数的图象过点(2,-4),则它的表达式为y=-2x.分析 设正比例函数的解析式为y=kx(k≠0),再把点(2,-4)代入求出k的值即可.
解答 解:设正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象过点(2,-4),
∴-4=2k.解得k=-2.
故答案为:y=-2x.
点评 本题考查的是待定系数法求正比例函数的解析式,熟知正比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
6.为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度:
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高72.2cm的课桌,它们是否配套?为什么?
| 椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
| 桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(2)现有一把高38cm的椅子和一张高72.2cm的课桌,它们是否配套?为什么?
3.某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
| 售价x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
10. 如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )
 如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -2<k<0 | B. | -2<k<$\frac{1}{8}$ | C. | -2<k<-1 | D. | -2<k<$\frac{1}{4}$ |
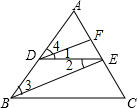 完成下面的证明.
完成下面的证明.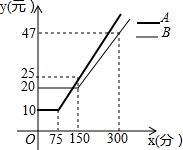 某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.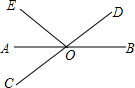 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.