题目内容
11.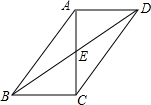 如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.
如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.
分析 由平行四边形的性质得出CE=$\frac{1}{2}$AC,BE=$\frac{1}{2}$BD,根据勾股定理求出AC,得出CE,再根据勾股定理求出BE,即可得出BD.
解答 解:∵四边形ABCD是平行四边形,
∴CE=$\frac{1}{2}$AC,BE=$\frac{1}{2}$BD,
∵AC⊥BC,
∴∠ACB=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{13}^{2}-{5}^{2}}$=12,
∴CE=$\frac{1}{2}$AC=6,
∴BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$,
∴BD=2BE=2$\sqrt{61}$;
故答案为:2$\sqrt{61}$.
点评 本题考查了平行四边形的性质、勾股定理的运用;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知圆锥的底面半径为4cm,高为3cm,则圆锥的侧面积是( )
| A. | 20cm2 | B. | 20πcm2 | C. | 12πcm2 | D. | 10πcm2 |
19.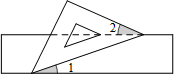 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )| A. | 30° | B. | 45° | C. | 25° | D. | 15° |
6.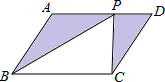 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 无法确定 |
16.下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
20.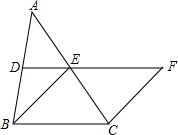 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
1. 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )| A. | BE=DF | B. | BF=DE | C. | AE=CF | D. | ∠1=∠2 |
 如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.