题目内容
19．
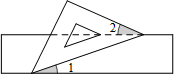如图，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上，则∠1+∠2=（ ）| A． | 30° | B． | 45° | C． | 25° | D． | 15° |
分析 先根据平行线的性质得∠1=∠3，然后利用∠1+∠3=45°求解．
解答 解：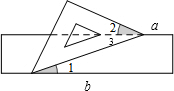
如图，
∵a∥b，
∴∠1=∠3，
∵∠1+∠3=45°，
∴∠1+∠2=45°．
故选B．
点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
10．
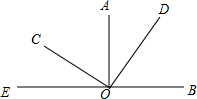如图，已知AO⊥BE于O点，CO⊥DO于O点，∠BOC=α，则∠AOD的度数为（ ）
如图，已知AO⊥BE于O点，CO⊥DO于O点，∠BOC=α，则∠AOD的度数为（ ）| A． | α-90° | B． | 2α-90° | C． | 180°-α | D． | 2α-180° |
7．在△ABC中，∠ABC=30°，∠BAC=70°．在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）
| A． | 7条 | B． | 8条 | C． | 9条 | D． | 10条 |
4．下列运算正确的是（ ）
| A． | $\sqrt{（-11）^{2}}$=-11 | B． | 2$\sqrt{2}$-$\sqrt{2}$=1 | ||
| C． | （-$\sqrt{2}$）2=2 | D． | $\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5 |
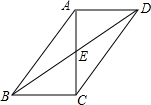如图，在?ABCD中，对角线AC，BD交于点E，AC⊥BC，若BC=5，AB=13，则BD的长是2$\sqrt{61}$．
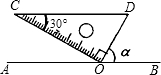如图，一块含有60°三角板的顶点O在直线AB上，CD∥AB．则∠α=60度．
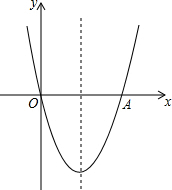如图，抛物线y=x2-4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．