题目内容
3. 如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发$\frac{4}{3}$或6秒直线CD恰好与⊙B相切.
分析 根据直线与圆相切和勾股定理,圆的半径与BC的关系,注意有2种情况解答即可.
解答 解:当直线与圆相切时,点C在圆的左侧,
∵∠DCB=30°,直线CD与⊙B相切,
∴2DB=BC,
即2(1+t)=10-4t,
解得:t=$\frac{4}{3}$,
当直线与圆相切时,点C在圆的右侧,
∵∠DCB=30°,直线CD与⊙B相切,
∴2DB=BC,
即2(1+t)=4t-10,
解得:t=6,
故答案为:$\frac{4}{3}$或6.
点评 本题考查了直线与圆的位置关系,关键是根据含30°的直角三角形中30°所对的边是斜边的一半进行分析.

练习册系列答案
相关题目
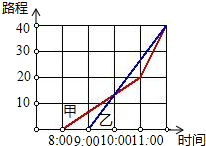 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: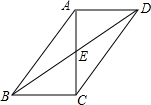 如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.
如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.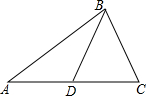 如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.
如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.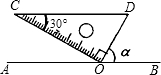 如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.
如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.
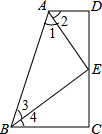 如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,求证:AD+BC=AB.
如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,求证:AD+BC=AB. 如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.
如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.