题目内容
1. 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )| A. | BE=DF | B. | BF=DE | C. | AE=CF | D. | ∠1=∠2 |
分析 利用平行四边形的性质以及全等三角形的判定分别得出三角形全等,再进行选择即可.
解答 解:A、当BE=FD,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),故此选项错误;
C、当AE=CF无法得出△ABE≌△CDF,故此选项符合题意;
B、当BF=ED,
∴BE=DF,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),故此选项错误;
D、当∠1=∠2,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中
$\left\{\begin{array}{l}{∠1=∠2}\\{AB=CD}\\{∠ABE=∠CDF}\end{array}\right.$,
∴△ABE≌△CDF(ASA),故此选项错误;
故选C.
点评 本题考查了平行四边形的性质以及全等三角形的判定等知识,熟练掌握全等三角形的判定方法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.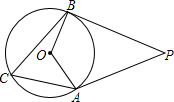 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为( )| A. | 65° | B. | 130° | C. | 50° | D. | 100° |
2.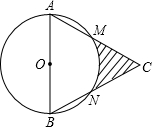 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )| A. | 9$\sqrt{3}$-6π | B. | 18$\sqrt{3}$-6π | C. | 12$\sqrt{3}$-3π | D. | 12$\sqrt{3}$-6π |
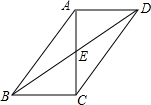 如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.
如图,在?ABCD中,对角线AC,BD交于点E,AC⊥BC,若BC=5,AB=13,则BD的长是2$\sqrt{61}$.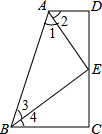 如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,求证:AD+BC=AB.
如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,求证:AD+BC=AB.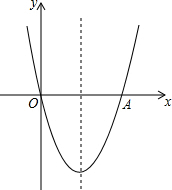 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q. 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.
如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25. 如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.
如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB∥EF,AB=EF.求证:BC=FD.