题目内容
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |
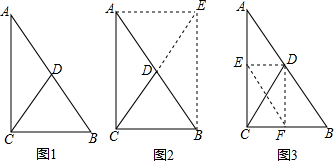
分析 延长CD至E,使DE=CD,连接AE、BE,根据平行四边形的判定定理证明四边形ACBE是平行四边形,根据矩形的判定定理证明四边形ACBE是矩形,根据矩形的对角线相等证明结论.
解答  证明:如图2,延长CD至E,使DE=CD,连接AE、BE;
证明:如图2,延长CD至E,使DE=CD,连接AE、BE;
又∵AD=DB,
∴四边形ACBE是平行四边形,
又∵CD=$\frac{1}{2}$AB,CD=$\frac{1}{2}$CE,
∴四边形ACBE是矩形,
∴∠ACB=90°,
∴△ABC为直角三角形.
点评 本题考查的是矩形的判定和性质,正确作出辅助线、灵活运用矩形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
5.某企业今年1月份产值为a万元,2月份比1月份减少了10%,3月份又开始了回暖,已知3,4月份平均月增长率为10%,则4月份的产值是( )
| A. | (a-10%)(a+20%)万元 | B. | a(1-10%)(1+10%)2万元 | ||
| C. | a(1-10%)(1+20%)万元 | D. | a(1+10%)万元 |
15.下列命题中:①4的平方根是±2;②16的算术平方根是2;③若x2=9,则x=3;④若x3=-8,则x=-2.其中是真命题的有( )
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
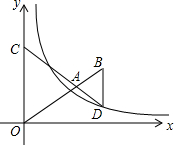 如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )
如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )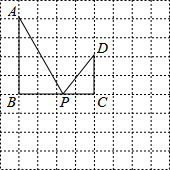 在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.
在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.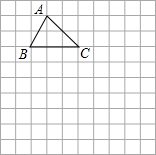 在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)
在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)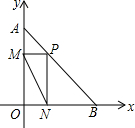 如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.
如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.