题目内容
1.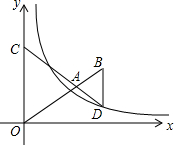 如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )
如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
分析 过A作直线AM⊥y轴,交OA于M,交BD于N,根据题意得到AM=$\frac{\sqrt{3}}{2}$OA,AN=$\frac{\sqrt{3}}{2}$AB,AM+AN=$\frac{\sqrt{3}}{2}$(0A+AB),从而求得D的横坐标为:$\frac{\sqrt{3}}{2}$(0A+AB),纵坐标为$\frac{1}{2}$(OA-AB),根据OA2-AB2=8$\sqrt{3}$即可求出k的值.
解答 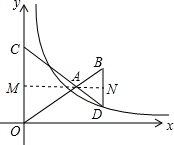 解:过A作直线AM⊥y轴,交OA于M,交BD于N,
解:过A作直线AM⊥y轴,交OA于M,交BD于N,
由题意可知,AM=$\frac{\sqrt{3}}{2}$OA,AN=$\frac{\sqrt{3}}{2}$AB,
∴AM+AN=$\frac{\sqrt{3}}{2}$(0A+AB),
∴D的横坐标为:$\frac{\sqrt{3}}{2}$(0A+AB),
∵D的纵坐标为$\frac{OC-BD}{2}$=$\frac{OA-AB}{2}$,
∴k=$\frac{\sqrt{3}}{2}$(OA+AB)•$\frac{1}{2}$(OA-AB)=$\frac{\sqrt{3}}{4}$(OA2-AB2),
∵OA2-AB2=8$\sqrt{3}$,
∴k=$\frac{\sqrt{3}}{4}$×8$\sqrt{3}$=6,
故选:B.
点评 本题考查的是等边三角形的性质和待定系数法求反比例函数的解析式,正确表示出点D的坐标是解题的关键,解答时,注意因式分解的运用.

练习册系列答案
相关题目
10.某学习小组,在探究1+$\frac{2}{x}$的性质时,得到了如下数据:
根据表格中的数据,做出了四个推测:
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| x | 1 | 10 | 100 | 1000 | 10000 | … |
| 1+$\frac{2}{x}$ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
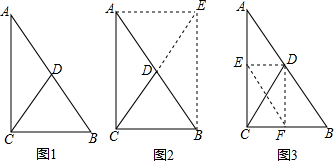
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |

11.tan60°的值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
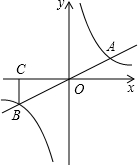 如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.