题目内容
18.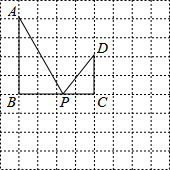 在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.
在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.(1)设BP=x,用含字母x的代数式分别表示线段AP,DP的长,并求当x=2的时候,AP+DP的值;
(2)AP+DP是否存在最小值?若存在,求出其最小值.
分析 (1)分别用x表示出BP、CD的长度,再根据勾股定理求出AP、DP的长即可;
(2)作点A关于BC的对称点A′,连接A′D,再由对称的性质及勾股定理即可求解.
解答 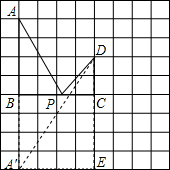 解:(1)由题意结合图形知:
解:(1)由题意结合图形知:
AB=4,BP=x,CP=4-x,CD=2,
∴AP=$\sqrt{A{P}^{2}+B{P}^{2}}$=$\sqrt{{x}^{2}+16}$,
DP=$\sqrt{P{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}{+(4-x)}^{2}}$=$\sqrt{{x}^{2}-8x+20}$;
当x=2时,AP+DP=$\sqrt{20}$+$\sqrt{8}$=2$\sqrt{5}$+2$\sqrt{2}$;
(2)存在.
如图,作点A关于BC的对称点A′,连接A′D,
∴A′E=4,DE=6,
则A′D=$\sqrt{A′{E}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=$\sqrt{52}$=$2\sqrt{13}$,
∴最小值为2$\sqrt{13}$.
点评 本题主要考查的是最短线路问题及勾股定理,根据题意画出图形是解答此类题目的关键.

练习册系列答案
相关题目
10.某学习小组,在探究1+$\frac{2}{x}$的性质时,得到了如下数据:
根据表格中的数据,做出了四个推测:
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| x | 1 | 10 | 100 | 1000 | 10000 | … |
| 1+$\frac{2}{x}$ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列命题中是假命题的是( )
| A. | △ABC中,若∠A=∠C-∠B,则△ABC是直角三角形 | |
| B. | △ABC中,若a2=b2-c2,则△ABC是直角三角形 | |
| C. | △ABC中,若a:b:c=5:12:13,则△ABC是直角三角形 | |
| D. | △ABC中,若∠A,∠B,∠C的度数比是3:4:5,则△ABC是直角三角形 |
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
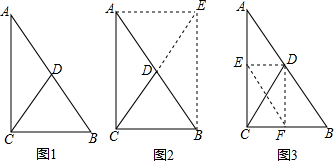
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |

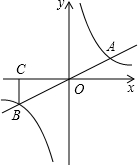 如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.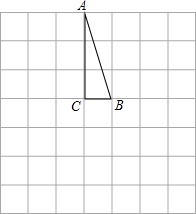 如图所示,在方格图中有三角形ABC(每个小方格的边长为1个单位长度)
如图所示,在方格图中有三角形ABC(每个小方格的边长为1个单位长度)