题目内容
17.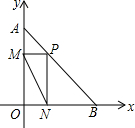 如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.
如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.
分析 首先连接OP,易得四边形ONPM是矩形,即可得在Rt△AOB中,当OP⊥AB时OP最短,即MN最小,然后利用勾股定理与三角形的面积的求解,可求得MN的长.
解答 解:如图,连接OP.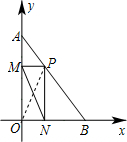
由已知可得:∠PMO=∠MON=∠ONP=90°.
∴四边形ONPM是矩形.
∴OP=MN,
在Rt△AOB中,当OP⊥AB时OP最短,即MN最小.
∵A(0,4),B(3,0),即AO=4,BO=3,
根据勾股定理可得AB=5.
∵S△AOB=$\frac{1}{2}$AO•BO=$\frac{1}{2}$AB•OP,
∴OP=$\frac{12}{5}$.
∴MN=$\frac{12}{5}$.
即当点P运动到使OP⊥AB于点P时,MN最小,最小值为$\frac{12}{5}$;
故答案为$\frac{12}{5}$.
点评 此题考查了矩形的判定与性质、勾股定理与三角形面积问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
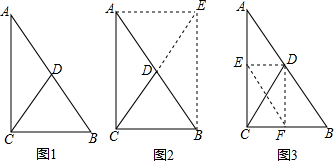
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |

11.tan60°的值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7.小亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下表是上周送出的20筐新鲜蔬菜的质量记录,每筐以25千克为标准重量,求上周送出20筐新鲜蔬菜的总重量.
| 筐 数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准重量比较(千克) | -0.8 | +0.6 | -0.5 | -0.4 | +0.5 | -0.3 |
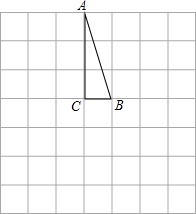 如图所示,在方格图中有三角形ABC(每个小方格的边长为1个单位长度)
如图所示,在方格图中有三角形ABC(每个小方格的边长为1个单位长度)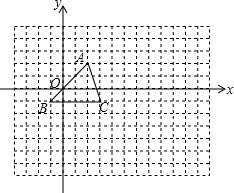 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).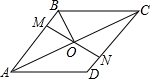 如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.
如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.