题目内容
3.计算(1)运用乘法公式简便运算:98×102
(2)2-2+($\frac{2}{3}$)0+(-0.2)2014×52014.
分析 (1)利用平方差公式计算即可;
(2)先算0指数幂,负指数幂,以及积的乘方计算,再算加法.
解答 解:(1)98×102
=(100-2)×(100+2)
=10000-4
=9996;
(2)原式=$\frac{1}{4}$+0+1
=$\frac{5}{4}$.
点评 此题考查整式的混合运算,掌握运算顺序与计算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.-3是3的( )
| A. | 平方根 | B. | 倒数 | C. | 相反数 | D. | 绝对值 |
10.某学习小组,在探究1+$\frac{2}{x}$的性质时,得到了如下数据:
根据表格中的数据,做出了四个推测:
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| x | 1 | 10 | 100 | 1000 | 10000 | … |
| 1+$\frac{2}{x}$ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
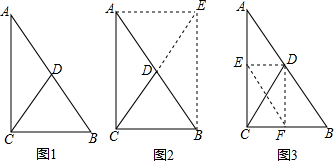
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |

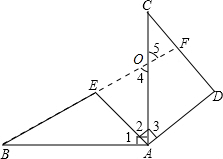 如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.
如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.