题目内容
15.下列命题中:①4的平方根是±2;②16的算术平方根是2;③若x2=9,则x=3;④若x3=-8,则x=-2.其中是真命题的有( )| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
分析 根据平方根的概念、算术平方根的概念和立方根的概念进行判断即可得到答案.
解答 解:4的平方根是±2,①正确;
16的算术平方根是4,②错误;
若x2=9,则x=±3,③错误;
若x3=-8,则x=-2,④正确,
故选:B.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
8.-3是3的( )
| A. | 平方根 | B. | 倒数 | C. | 相反数 | D. | 绝对值 |
3.下列命题中是假命题的是( )
| A. | △ABC中,若∠A=∠C-∠B,则△ABC是直角三角形 | |
| B. | △ABC中,若a2=b2-c2,则△ABC是直角三角形 | |
| C. | △ABC中,若a:b:c=5:12:13,则△ABC是直角三角形 | |
| D. | △ABC中,若∠A,∠B,∠C的度数比是3:4:5,则△ABC是直角三角形 |
10.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
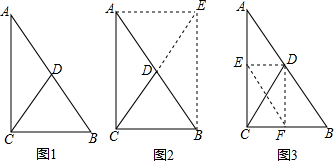
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
通过探究,小明发现这个猜想也成立,以下是小明的证明过程:
已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=$\frac{1}{2}$AB
求证:△ABC为直角三角形
证明:由条件可知,AD=BD=CD
则∠A=∠DCA,∠B=∠DCB
又∵∠A+∠DCA+∠B+∠DCB=180°
∴∠DCA+∠DCB=90°
爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:
| 证法一:如图2,延长CD至E,使DE=CD,连接AE、BE; 又∵AD=DB |
| 证法二:如图3,分别作AC、BC的中点E,F,连接DE、DF、EF; 则DE、DF、EF为△ABC的中位线 |

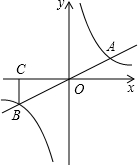 如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.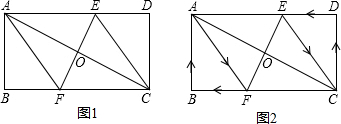
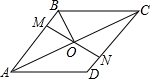 如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.
如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.