题目内容
15．若关于x的方程$\frac{1}{x-1}-\frac{a}{2-x}=\frac{2（a+1）}{（x-1）（x-2）}$无解，则a的值为（ ）| A． | $-\frac{3}{2}$或-2 | B． | $-\frac{3}{2}$或-1 | C． | $-\frac{3}{2}$或-2或-1 | D． | -2或-1 |
分析 先去分母得到关于x的整式方程，然后根据分式方程无解得到关于a的方程，从而求得a的值．
解答 解：去分母得：x-2+a（x-1）=2a+2．
整理得：（a+1）x=3a+4．
当a+1=0时，解得：a=-1，此时分式方程无解；
当a+1≠0时，x=$\frac{3a+4}{a+1}$．
当x=1时，$\frac{3a+4}{a+1}$=1．解得：a=-$\frac{3}{2}$，此时分式方程无解；
当x=2时，$\frac{3a+4}{a+1}$=2，解得：a=-2，此时分式方程无解．
故选：C．
点评 本题主要考查的是分式方程的解，掌握分式方程无解的条件是解题的关键．
练习册系列答案
相关题目
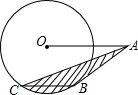如图，⊙O的半径为4，OA=8，AB切⊙O于B，弦BC∥OA，连接AC，则图中阴影部分的面积为$\frac{8}{3}$π．
10．
如图，P是⊙O外一点，PA、PB是⊙O的两条切线，切点分别为A、B，连接AB，OP相交于点C，OP与⊙O相交于点D，则下列结论不正确的是（ ）
如图，P是⊙O外一点，PA、PB是⊙O的两条切线，切点分别为A、B，连接AB，OP相交于点C，OP与⊙O相交于点D，则下列结论不正确的是（ ）| A． | PA=PB | B． | ∠APO=∠BPO | C． | OC=CD | D． | ∠OAP=90° |
甲、乙两人都从光明学校出发，去距离光明学校1500m远的篮球馆打球，他们沿同一条道路匀速行走，乙比甲晚出发4min．设甲行走的时间为t（单位：min），甲、乙两人相距y（单位：m），表示y与t的函数关系的图象如图所示，根据图中提供的信息，下列说法：