题目内容
20.计算$\frac{1}{2}$+($\frac{1}{3}$+$\frac{2}{3}$)+($\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$)+$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$+…+($\frac{1}{50}$+$\frac{2}{50}$+$\frac{3}{50}$+…+$\frac{49}{50}$)=( )| A. | 612 | B. | 612.5 | C. | 613 | D. | 613.5 |
分析 首先根据$\frac{1}{2}$=$\frac{1}{2}$,$\frac{1}{3}$+$\frac{2}{3}$=1,$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$=1$\frac{1}{2}$,$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$=2,…,判断出$\frac{1}{2}$、$\frac{1}{3}$+$\frac{2}{3}$、$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$、$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$、…、$\frac{1}{50}$+$\frac{2}{50}$+$\frac{3}{50}$+…+$\frac{49}{50}$构成了$\frac{1}{2}$为首项,$\frac{1}{2}$为公差的等差数列;然后根据等差数列的求和方法,求出算式的值是多少即可.
解答 解:$\frac{1}{2}$+($\frac{1}{3}$+$\frac{2}{3}$)+($\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$)+$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$+…+($\frac{1}{50}$+$\frac{2}{50}$+$\frac{3}{50}$+…+$\frac{49}{50}$)
=$\frac{1}{2}$+1+1$\frac{1}{2}$+2+…+24$\frac{1}{2}$
=($\frac{1}{2}+24\frac{1}{2}$)×49÷2
=25×49÷2
=612.5
故选:B.
点评 此题主要考查了有理数的加法,以及等差数列的求和方法,要熟练掌握,解答此题的关键是判断出$\frac{1}{2}$、$\frac{1}{3}$+$\frac{2}{3}$、$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$、$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$、…、$\frac{1}{50}$+$\frac{2}{50}$+$\frac{3}{50}$+…+$\frac{49}{50}$构成了$\frac{1}{2}$为首项,$\frac{1}{2}$为公差的等差数列.

| A. | -1的立方根是-1 | B. | 1的平方根是1 | C. | $\sqrt{2}$是2的平方根 | D. | -3是9的平方根 |
| A. | $-\frac{3}{2}$或-2 | B. | $-\frac{3}{2}$或-1 | C. | $-\frac{3}{2}$或-2或-1 | D. | -2或-1 |
| A. | (x+2)(x-3)=0 | B. | x2-x+6=0 | C. | x2-5x-1=0 | D. | x2+x-6=0 |
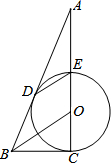 如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC. 甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.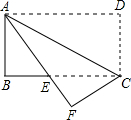 如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.
如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.