题目内容
3.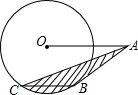 如图,⊙O的半径为4,OA=8,AB切⊙O于B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{8}{3}$π.
如图,⊙O的半径为4,OA=8,AB切⊙O于B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{8}{3}$π.
分析 △OBC与△BCA是同底等高,则它们的面积相等,因此阴影部分的面积实际是扇形OCB的面积;扇形OCB中,已知了半径的长,关键是圆心角∠COB的度数.在Rt△ABO中,根据OB、OA的长,即可求得∠BOA的度数;由于OA∥BC,也就求得了∠OBC的度数,进而可在△COB中求出∠COB的度数,由此可根据扇形的面积公式求出阴影部分的面积.
解答 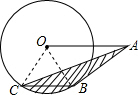 解:连接OB、OC
解:连接OB、OC
OB是半径,AB是切线,
∵OB⊥AB,
∴∠ABO=90°,
∴sinA=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴∠A=30°,
∵OC=OB,BC∥OA,
∴∠OBC=∠BOA=60°,
∴△OBC是等边三角形,
因此S阴影=S扇形CBO=$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}$π.
故答案为$\frac{8}{3}$π.
点评 本题利用了平行线的性质,同底等高的三角形面积相等,切线的概念,正弦的概念,扇形的面积公式求解.

练习册系列答案
相关题目
14.下列各式不是方程的是( )
| A. | 3x2+4=5 | B. | m+2n=0 | C. | x=-3 | D. | 4y>3 |
15.若关于x的方程$\frac{1}{x-1}-\frac{a}{2-x}=\frac{2(a+1)}{(x-1)(x-2)}$无解,则a的值为( )
| A. | $-\frac{3}{2}$或-2 | B. | $-\frac{3}{2}$或-1 | C. | $-\frac{3}{2}$或-2或-1 | D. | -2或-1 |
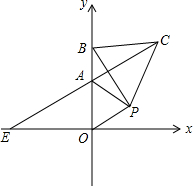 如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC.
如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC. 如图是一个正方体的展开图,标注了字母a的面是正方体的正面.如果正方体相对两个面上的式子的值相等,求(y-x)2015的值.
如图是一个正方体的展开图,标注了字母a的面是正方体的正面.如果正方体相对两个面上的式子的值相等,求(y-x)2015的值. 甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.