题目内容
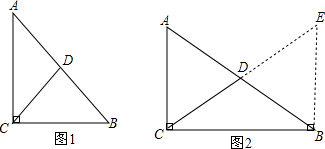
4.在Rt△ABC中,∠ACB=90°,点D为AB中点,连接CD.(1)如图1所示,AC=BC,求证:AB=2CD;
(2)若AC≠BC(如图2所示).(1)中结论是否仍然成立?若成立.请证明;若不成立,请说明理由.
分析 (1)由等腰直角三角形的性质得到∠B=45°,根据等腰三角形的性质得到CD⊥AB,于是得到∠DCB=45°,求得CD=BD,于是得到结论;
(2)如图1,取AC中点E,连接DE,根据三角形的中位线的性质和线段垂直平分线的性质即可得到结论.
解答 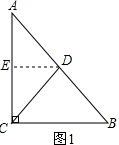 证明:(1)∵∠ACB=90°,AC=BC,
证明:(1)∵∠ACB=90°,AC=BC,
∴∠B=45°,
∵点D为AB中点,
∴CD⊥AB,
∴∠DCB=45°,
∴∠B=∠DCB,
∴CD=BD,
∵AB=2BD,
∴AB=2CD;
(2)如图1,取AC中点E,连接DE,
∵D是AB中点,
∴AD=BD,
∴DE∥BC,
∵∠ACB=90°,
∠AED=∠ACB=90°,
DE是AC的垂直平分线,
∴AD=CD,
∴AB=AD+BD=2AD=2CD.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的性质,三角形的中位线的性质,熟练三角形的中位线的性质是解题的关键.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
14.下列方程中有两个相等实数根的是( )
| A. | x2+3=0 | B. | x2+5x=0 | C. | (x+3)(x-1)=0 | D. | (x+3)2=0 |
 我们知道,A、B两点所对的数分别为a,b,则AB的距离为|a-b|,试求|x-3|+|x+5|的最小值.
我们知道,A、B两点所对的数分别为a,b,则AB的距离为|a-b|,试求|x-3|+|x+5|的最小值.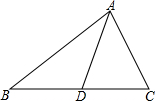 如图,在△ABC中,点D是BC边的中点,已知AB=8cm,AC=6cm,△ABC的面积是12cm2.
如图,在△ABC中,点D是BC边的中点,已知AB=8cm,AC=6cm,△ABC的面积是12cm2.