题目内容
17.△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=90°;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由.
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是60°+α或60°-α或60°;.

分析 (1)连接PC,由三角形的外角性质即可得出结论;
(2)①根据题意画出图形即可;
②由三角形的外角性质即可得出结论;
(3)分三种情况讨论,由三角形的外角性质即可得出结论.
解答  解;(1)∠PEB+∠PDA=90°;理由如下;
解;(1)∠PEB+∠PDA=90°;理由如下;
连接PC,如图1所示
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角
∴∠PDA=∠1+∠2,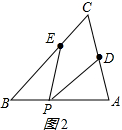
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+30°=90°
故答案为:90°;
(2)①如图2所示;
②连接PC,如图3所示:
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角,
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+α;
∴∠PEB+∠PDA=60°+α;
(3)分三种情况:
①如图4所示:
连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2+∠3,∠PDA=∠1+∠2
∴∠PEB-∠PDA=∠ACB+∠3=60°+α;
②如图5所示:连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2+∠3,
∴∠PEB-∠PDA=∠ACB-∠3=60°-α;
③如图6所示:P、D、E在同一条直线上,连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2,
∴∠PEB-∠PDA=∠ACB=60°;
综上所述:如果点P在线段BA的延长线上运动,
∠PEB与∠PDA之间的数量关系是60°+α或60°-α或60°;
故答案为:60°+α或60°-α或60°.
点评 本题是三角形综合题目,考查了三角形的外角性质、角之间的数量关系;本题综合性强,有一定难度,通过作辅助线运用三角形的外角性质是解决问题的关键,注意(3)中分类讨论.

 在矩形ABCD中,AB=6,BC=4,动点P从点B出发,沿着B→C→D→A点停止,设点P运动的路程为x,△ABP的面积为y,请用x表示y.
在矩形ABCD中,AB=6,BC=4,动点P从点B出发,沿着B→C→D→A点停止,设点P运动的路程为x,△ABP的面积为y,请用x表示y.
 QQ好友的等级会用一些图标来表示,如图是小明同学的两个好友的等级示例,小明想知道一个太阳
QQ好友的等级会用一些图标来表示,如图是小明同学的两个好友的等级示例,小明想知道一个太阳  和一个月亮
和一个月亮 所表示的等级.
所表示的等级. 已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题:
已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题: 如图,在平面直角坐标系中,已知点A(2,0),P是函数y=x(x>0)图象上一点,PQ⊥AP交y轴于点Q.设点P的横坐标为a,点Q的纵坐标为b,若OP<10$\sqrt{2}$,求b的取值范围.
如图,在平面直角坐标系中,已知点A(2,0),P是函数y=x(x>0)图象上一点,PQ⊥AP交y轴于点Q.设点P的横坐标为a,点Q的纵坐标为b,若OP<10$\sqrt{2}$,求b的取值范围.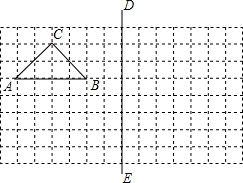 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题: