题目内容
5.如图,在平面直角坐标系xOy中,已知A(3,3),B(9,0),若有一动点M从原点出发,沿x轴正半轴向点B运动,过点M作直线l⊥x轴.(1)如图①,若直线l与线段OA相交于点N,且M(2,0),求此时MN的长;
(2)如图②,若直线l与线段AB相交于点N,且MN=2,求此时点M的坐标.

分析 (1)作AC⊥x轴,垂足为C,证明△OMN∽△OCA,由相似三角形的性质可求得MN的长;(2)与(1)同法.
解答 解:(1)如图①所示:
作AC⊥x轴,垂足为C
∵直线l⊥x轴,
∴△OMN∽△OCA,
∴$\frac{MN}{AC}=\frac{OM}{OC}$,其中,AC=3,OM=2,OC=3
∴MN=2
即:MN的长为2
(2)如图②所示:做AD⊥x轴,垂足为点D,设M的坐标为(a,0)
同(1)可知:△BAD∽△BNM,
∴$\frac{AD}{MN}=\frac{BD}{BM}$,其中AD=3,MN=2,BD=9-3=6,BM=9-a,
∴a=5,
∴点M的坐标为(5,0)
点评 本题考查了坐标与图形的性质,解题的关键是理解点的坐标的意义及相似三角形的判定及应用.

练习册系列答案
相关题目
16.图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示,根据图中的信息,回答问题:
(1)根据图2补全表格:
(2)如表反映的两个变量中,自变量是旋转时间x,因变量是高度y;
(3)根据图象,摩天轮的直径为65m,它旋转一周需要的时间为6min.

(1)根据图2补全表格:
| 旋转时间x/min | 0 | 3 | 6 | 8 | 12 | … |
| 高度y/m | 5 | 70 | 5 | 54 | 5 | … |
(3)根据图象,摩天轮的直径为65m,它旋转一周需要的时间为6min.

 如图,在正方形ABCD中,点E为边AB上任一点(与点A,B不重合),连接CE,过点D作DF⊥CE于点F,连接AF并延长交BC边于点G,连接EG,若正方形边长为4,GC=$\frac{2}{3}$AE,则GE=$\frac{4}{9}$$\sqrt{85}$.
如图,在正方形ABCD中,点E为边AB上任一点(与点A,B不重合),连接CE,过点D作DF⊥CE于点F,连接AF并延长交BC边于点G,连接EG,若正方形边长为4,GC=$\frac{2}{3}$AE,则GE=$\frac{4}{9}$$\sqrt{85}$. 求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数.
求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数. 已知一次函数y=-x+3与x轴、y轴分别交于A、B两点.
已知一次函数y=-x+3与x轴、y轴分别交于A、B两点.
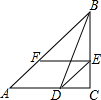 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF.
如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF. 如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点.
如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点.