题目内容
9. 已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题:
已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题:(1)当x>0时,求y的取值范围;
(2)当2≤x≤5时,求y的取值范围.
分析 (1)由题意可知当x=1时,y有最小值2,则可知在第一象限内y的取值范围;
(2)当x>1时,y随x的增大而增大,则可求得y取值范围.
解答 解:
(1)由图象可知当x>0时,函数最小值为2,
∵当x=1时y有最小值2,
∴当x>0时,y≥2;
(2)由图象可知当x>1时,y随x的增大而增大,
∴当2≤x≤5时,当x=2时,y有最小值,y=2+$\frac{1}{2}$=$\frac{5}{2}$,
当x=5时,y有最大值,y=5+$\frac{1}{5}$=$\frac{26}{5}$,
∴当2≤x≤5时,求y的取值范围为$\frac{5}{2}$≤y≤$\frac{26}{5}$.
点评 本题主要考查反比例函数的性质,求得当x>1时y随x的增大而增大是解题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18.柑橘是万州农业一大优势传统产业,柑橘产业是万州经济发展和移民安稳致富的支柱产业,也是保护三峡岸区生态环境的重要产业,做好柑橘产业发展工作意义十分重大.某水果经销商到万州采购柑橘,他看中了甲、乙两家的某种品质相近的柑橘,零售价都为6元/千克,批发价各不相同.
甲家规定:批发数量不超过100千克,全部按零售价的90%优惠;批发数量超过100千克但不超过200千克,全部按零售价的85%优惠;超过200千克的按零售价的80%优惠.
乙家的规定如下表:
(1)如果他批发80千克柑橘,则他在甲、乙两家批发各需花多少元?
(2)现在他要批发180千克柑橘,你能帮助他选择在哪家批发更优惠吗?请说明理由.
(3)如果他批发x千克柑橘(200<x<250),则他在甲、乙两家批发各需要多少元?(用含x的代数式表示)
甲家规定:批发数量不超过100千克,全部按零售价的90%优惠;批发数量超过100千克但不超过200千克,全部按零售价的85%优惠;超过200千克的按零售价的80%优惠.
乙家的规定如下表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)现在他要批发180千克柑橘,你能帮助他选择在哪家批发更优惠吗?请说明理由.
(3)如果他批发x千克柑橘(200<x<250),则他在甲、乙两家批发各需要多少元?(用含x的代数式表示)
 如图,△ABC中,∠C=90°,D为BC的中点,∠ADC=60°,AC=$\sqrt{3}$.求△ABD的周长.
如图,△ABC中,∠C=90°,D为BC的中点,∠ADC=60°,AC=$\sqrt{3}$.求△ABD的周长. 已知一次函数y=-x+3与x轴、y轴分别交于A、B两点.
已知一次函数y=-x+3与x轴、y轴分别交于A、B两点.
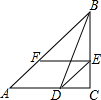 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF.
如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF.