题目内容
4.在二次函数y1=ax2+bx+c中,部分x、y的对应值如表:| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 | … |
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
分析 (1)由题目所给表格可观察得出答案;
(2)可先求得二次函数解析式,联立两函数解析式可求得两函数图象的交点坐标,可画出两函数图象,则可求得答案.
解答 解:
(1)由表可知当x=1时,y有最大值,
∴二次函数图象开口向下,其顶点坐标为(1,2);
(2)∵抛物线顶点坐标为(1,2),
∴设抛物线解析式为y=a(x-1)2+2,
∵当x=0时,y=1,
∴1=a+2,解得a=-1,
∴抛物线解析式为y1=-(x-1)2+2=-x2+2x+1,
联立两函数解析式可得$\left\{\begin{array}{l}{y=-x+3}\\{y=-{x}^{2}+2x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
两函数图象如图所示: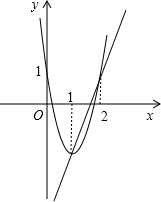
当y2在y1的图象下方时,结合图象x<1或x>2,
故答案为:x<1或x>2.
点评 本题主要考查二次函数的性质和图象,掌握二次函数的性质是解题的关键,注意数形结合.

练习册系列答案
相关题目
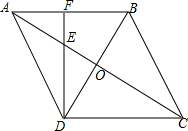 如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.
如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.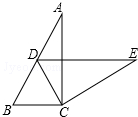 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为60°.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为60°.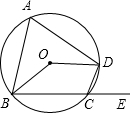 如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°.
如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度?66°.
如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度?66°.