题目内容
19.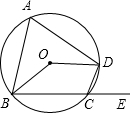 如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°.
如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°.
分析 由∠BOD=138°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠A的度数,又由圆的内接四边四边形的性质,求得∠BCD的度数,继而求得∠DCE的度数
解答 解:∵∠BOD=138°,
∴∠A=$\frac{1}{2}$∠BOD=69°,
∴∠BCD=180°-∠A=111°,
∴∠DCE=180°-∠BCD=69°.
故答案为:69°.
点评 此题考查了圆周角定理与圆的内接四边形的性质.此题比较简单,解题的关键是注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半与圆内接四边形的对角互补定理的应用.

练习册系列答案
相关题目
4.在二次函数y1=ax2+bx+c中,部分x、y的对应值如表:
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 | … |
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
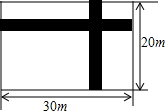 在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少?
在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少?