题目内容
9.先化简,再求值:(3x4-2x3)÷(-x)-(x-x2)•3x,其中x=-$\frac{1}{3}$.分析 先算乘法和除法,再合并同类项,最后代入求出即可.
解答 解:(3x4-2x3)÷(-x)-(x-x2)•3x
=-3x3+2x2-3x2+3x3
=-x2,
当x=-$\frac{1}{3}$时,原式=-(-$\frac{1}{3}$)2=-$\frac{1}{9}$.
点评 本题考查了整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
相关题目
4.在二次函数y1=ax2+bx+c中,部分x、y的对应值如表:
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 | … |
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
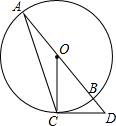 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接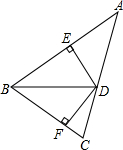 如图:BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18cm2,
如图:BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18cm2,