题目内容
12.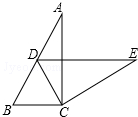 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为60°.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为60°.
分析 旋转角是∠BCD,只要证明△BCD是等边三角形即可.
解答  解:在Rt△ACB中,∵∠ACB=90°,∠A=30°,
解:在Rt△ACB中,∵∠ACB=90°,∠A=30°,
∴∠B=90°-∠A=60°,
∵CB=CD,
△BCD是等边三角形,
∴∠BCD=60°,
∴旋转角为60°,
故答案为60°.
点评 本题考查旋转的性质、等边三角形的判定、旋转角的定义等知识,解题的关键是利用旋转不变性,发现△BCD是等边三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.在二次函数y1=ax2+bx+c中,部分x、y的对应值如表:
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | 1 | $\frac{7}{4}$ | 2 | $\frac{7}{4}$ | 1 | -$\frac{1}{4}$ | -2 | … |
(2)作直线y2=-x+3,则当y2在y1的图象下方时,x的取值范围是x<1或x>2.
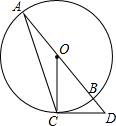 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接