题目内容
5.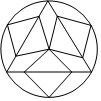 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
分析 由题意知:三个正方形的共用顶点即为圆的圆心,也是等边三角形的重心;可设等边三角形的边长为2x,作等边三角形,再根据三角形重心的性质即可得到正方形的对角线的长,求出正方形的边长,即可得出答案.
解答 解:如图,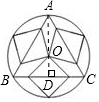
设圆的圆心为O,由题意知:三角形的重心以及三个正方形的共用顶点即为点O.
过A作AD⊥BC于D,则AD必过点O,且AO=2OD;
设△ABC的边长为2x,则BD=x,AD=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
OD=$\frac{\sqrt{3}}{3}$x;
∴正方形的边长为:$\frac{\sqrt{6}}{3}$x,
∴等边三角形与正方形的边长的比值是2x:$\frac{\sqrt{6}}{3}$x=$\sqrt{6}$,
故选C.
点评 此题考查的知识点有:轴对称图形、等边三角形及正方形的性质、三角形重心的性质等知识点,找到等边三角形和正方形边长的比例关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知一次函数y1=kx+2(k<0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A、B两点,则实数m的取值范围是( )
| A. | m>0 | B. | m<0 | C. | m>1 | D. | m<1 |
16.现有四张完全相同的卡片,上面分别标有数字0,1,2,3,把卡片背面朝上洗匀,然后从中随机抽取两张卡片组成一个两位数,则这个两位数是偶然的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
13.下列说法中错误的是( )
| A. | 零的相反数是零 | |
| B. | 任何有理数都有相反数 | |
| C. | a的相反数是-a | |
| D. | 表示相反意义的量的两个数互为相反数 |
20.用反证法证明“自然数a、b、c中恰有一个偶数”时,第一步应假设为( )
| A. | a、b、c都是奇数 | |
| B. | a、b、c或都是奇数或至少有两个偶数 | |
| C. | a、b、c都是偶数 | |
| D. | a、b、c中至少有两个偶数 |
10.下列说法中错误的是( )
| A. | 三角形的中线、角平分线,高线都是线段 | |
| B. | 有一个内角是直角的三角形是直角三角形 | |
| C. | 任意三角形的外角和都是360° | |
| D. | 三角形的一个外角大于任何一个内角 |
17.下列说话正确的是( )
| A. | 4的算术平方根是±2 | B. | 负数一定没有平方根 | ||
| C. | 平方根等于它本身的数有0和1 | D. | 0.9的算术平方根是0.3 |
14.若(x+6)(x-2)=x2+mx+n,则m.n分别为( )
| A. | m=4,n=12 | B. | m=-4,n=12 | C. | m=-4,n=-12 | D. | m=4,n=-12 |