题目内容
15.将4x2-4分解因式得4(x+1)(x-1).分析 原式提取4,再利用平方差公式分解即可.
解答 解:原式=4(x2-1)=4(x+1)(x-1),
故答案为:4(x+1)(x-1)
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.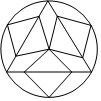 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
6. 在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放,则∠1的度数为( )
在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放,则∠1的度数为( )
 在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放,则∠1的度数为( )
在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放,则∠1的度数为( )| A. | 32° | B. | 36° | C. | 40° | D. | 42° |
3.一元二次方程x2-4x+5=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
20.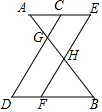 如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
 如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )| A. | $\frac{CG}{CD}$=$\frac{EH}{HF}$ | B. | $\frac{AG}{GB}$=$\frac{AC}{CD}$ | C. | $\frac{CE}{GH}$=$\frac{DF}{BG}$ | D. | $\frac{GC}{HE}$=$\frac{AC}{AE}$ |
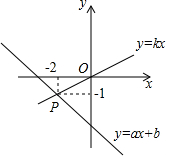 直线y=kx与y=ax+b的图象如图.
直线y=kx与y=ax+b的图象如图.  如图,在正方形ABCD中,AB=12,点E在边CD上,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长与CD相交于点G,若$\frac{EF}{AB}$=$\frac{1}{3}$,则FG的长度是$\frac{4\sqrt{10}}{5}$.
如图,在正方形ABCD中,AB=12,点E在边CD上,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长与CD相交于点G,若$\frac{EF}{AB}$=$\frac{1}{3}$,则FG的长度是$\frac{4\sqrt{10}}{5}$.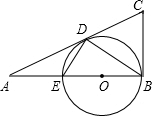 已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.


