题目内容
16．现有四张完全相同的卡片，上面分别标有数字0，1，2，3，把卡片背面朝上洗匀，然后从中随机抽取两张卡片组成一个两位数，则这个两位数是偶然的概率是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{5}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{2}$ |
分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与这个两位数是偶数的情况，再利用概率公式求解即可求得答案．
解答 解：画树状图得：
∵共有9种等可能的结果，这个两位数是偶数的有5种情况，
∴这个两位数是偶数的概率是：$\frac{5}{9}$，
故选：B．
点评 此题考查了列表法或树状图法求概率．注意0不能是十位数字，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
6．下列事件是必然事件的是（ ）
| A． | 打开电视机，正在播放《中国好声音》 | |
| B． | 上学路上经过十字路口遇上红灯 | |
| C． | 掷一枚均匀的硬币，正面朝上 | |
| D． | 从1、2、3、4、5这五个数中任取一个数，取到的数一定大于0 |
7．x12÷x3等于（ ）
| A． | x4 | B． | x15 | C． | x9 | D． | x36 |
4．在篮球比赛中，某队员连续10场比赛中每场的得分情况如下所示：
则这10场比赛中该队员得分的中位数和众数分别是（ ）
| 场次（场） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分（分） | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
| A． | 10，4 | B． | 10，13 | C． | 11，4 | D． | 12.5，13 |
11．已知直角三角形的周长是2+$\sqrt{6}$，斜边长为 2，则它的面积是（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | $\frac{1}{2}$$\sqrt{6}$ |
1．
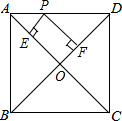如图，在正方形ABCD中，AB=1，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为 （ ）
如图，在正方形ABCD中，AB=1，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为 （ ）| A． | $\sqrt{2}$ | B． | 4 | C． | 2 | D． | $\frac{{\sqrt{2}}}{2}$ |
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为60°．
5．
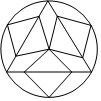如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与正方形的边长的比值为（ ）
如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与正方形的边长的比值为（ ）| A． | $\frac{{\sqrt{6}}}{2}$ | B． | 3 | C． | $\sqrt{6}$ | D． | $\frac{{3\sqrt{3}}}{2}$ |
6．
在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放，则∠1的度数为（ ）
在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放，则∠1的度数为（ ）| A． | 32° | B． | 36° | C． | 40° | D． | 42° |