题目内容
20.用反证法证明“自然数a、b、c中恰有一个偶数”时,第一步应假设为( )| A. | a、b、c都是奇数 | |
| B. | a、b、c或都是奇数或至少有两个偶数 | |
| C. | a、b、c都是偶数 | |
| D. | a、b、c中至少有两个偶数 |
分析 用反证法证明“自然数a、b、c中恰有一个偶数”时,第一步应假设为
解答 解:用反证法证明一个命题成立,首先假设命题的否定成立.
“自然数a、b、c中恰有一个偶数”的反面是“自然数a、b、c中至少两个偶数或都是偶数”.
故选B.
点评 本题考查了用反证法证明数学命题,要把所证的结论进行否定,证明反面不成立,从而证明所要证明的结论正确.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
11.已知直角三角形的周长是2+$\sqrt{6}$,斜边长为 2,则它的面积是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$$\sqrt{6}$ |
15.下列计算中,正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{5}+\sqrt{6}=\sqrt{11}$ | C. | $2+\sqrt{2}=2\sqrt{2}$ | D. | $\sqrt{2}+\sqrt{2}=2\sqrt{2}$ |
5.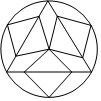 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
9.下列命题中的假命题是( )
| A. | 对顶角相等 | |
| B. | 内错角相等,两直线互相平行 | |
| C. | 同位角相等 | |
| D. | 平行于同一条直线的两直线互相平行 |
 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为60°.
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为60°.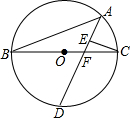 如图,BC为⊙O的直径,AB为⊙O的弦,D为$\widehat{BC}$的中点,CE⊥AD于E,AD交BC于点F,tan∠B=$\frac{1}{2}$
如图,BC为⊙O的直径,AB为⊙O的弦,D为$\widehat{BC}$的中点,CE⊥AD于E,AD交BC于点F,tan∠B=$\frac{1}{2}$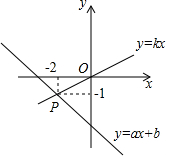 直线y=kx与y=ax+b的图象如图.
直线y=kx与y=ax+b的图象如图.