题目内容
6.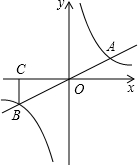 如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.(1)求k的值;
(2)求A、B两点的坐标.
分析 (1)根据反比例函数k的几何意义得到$\frac{1}{2}$•|k|=4,易得k=8;
(2)根据反比例函数与一次函数的交点问题,通过解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{8}{x}}\end{array}\right.$可得A、B两点的坐标.
解答 解:(1)∵△BOC的面积等于4,
∴$\frac{1}{2}$•|k|=4,
而k>0,
∴k=8;
(2)解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{8}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$,
所以A(4,2),B(-4,-2).
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
11.下列二次根式:$\sqrt{5},\sqrt{\frac{1}{3}},\sqrt{0.5a},-2\sqrt{{a^2}b},\sqrt{{x^2}+{y^2}}$中,是最简二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.下列命题中:①4的平方根是±2;②16的算术平方根是2;③若x2=9,则x=3;④若x3=-8,则x=-2.其中是真命题的有( )
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
16.正五边形的一个内角的度数为( )
| A. | 100° | B. | 108° | C. | 112° | D. | 120° |
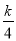 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.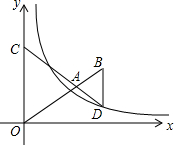 如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )
如图,△ACO和△ABD都是等边三角形,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点D,若OA2-AB2=8$\sqrt{3}$,则k的值为( )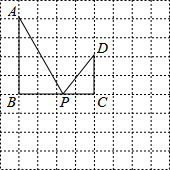 在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.
在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.